In order to meaningfully compare costs and benefits of lockdown, it is necessary to have some assumptions about the value of human life. There are different approaches that can be taken to this, such as using the (quality-adjusted) life year thresholds used by public heath systems to ‘price’ a year of healthy human life. Of course, it is popular and politically expedient to ignore the price of life issue, indeed some like to argue that human life is of infinite value. This is nonsense. Human life has a finite value, else we would have no basis to determine whether it made sense to approve treatments based on their cost and their medical merit.
Modelling life expectancy in terms of GDP
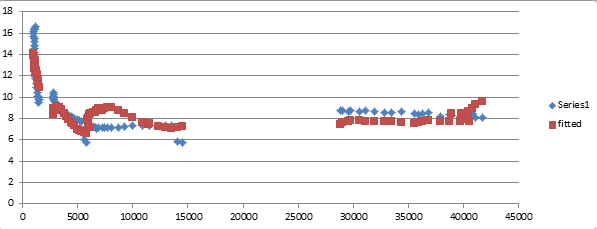
The approach I will take is slightly different here. I will attempt to model the relationship between GDP and life expectancy using a simple regression model for the EU-28 countries. The intuition is that higher GDP enables a prolongation of human life, through better diet, investment in workplace health and safety and investment in curative and preventative medicine. Over the relevant part of the curve, we should see a clear relationship emerge, which will allow us to understand what the cost in terms of life is, of reducing GDP. This can then be compared with the estimated benefits – also in terms of human life – of implementing a lockdown.
I use the data from Eurostat for 2018 GDP per capita in euros, (GDP), for life expectancy at age 1 (LE) to construct a simple regression model specified as follows
LE = a*GDP+b*GDP^2
The spreadsheet with the data is here. I exclude Luxembourg and Ireland because of well-known problems with the measurement of GDP. While other control variables are not included, in fact the institutional nature of the EU suggests that many other relevant factors (such as the design of the public health system, workplace health and safety rules, and other cultural factors) enjoy a certain degree of harmonisation.
The results of the regression are as below:
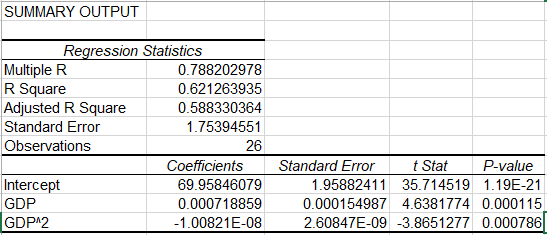
And show that both variables are statistically significant (high t Stat values), and that quite alot of the variation (around 60%) in LE can be explained by GDP/capita alone (high ‘Adjusted R Square’).
The coefficients in the last three rows imply:
(a) that in the absence of any GDP, life expectancy would be at 70 (intercept). Although this seems unreasonably high, suggesting more non-linearity in the relationship as income falls to the zero-threshold, it is not a big deal, however, as we are only concerned with the relationship over the relevant space, i.e. in terms of the GDP/capita of developed, Western countries.
(b) there is a positive relationship between GDP and Life Expectancy; namely that a one Euro increase in GDP/capita results in an increase in life expectancy of 0.0007 years. This is what we would expect to see.
(c) there is a negative relationship between GDP squared and Life Expectancy; namely that as the square of GDP rises by one euro, LE falls by 0.000000001 years. This is also what we would expect – the gains to life expectancy are limited, and at very high income levels, there may even be a reverse effect, due to stress from work, pollution or other lifestyle effects.
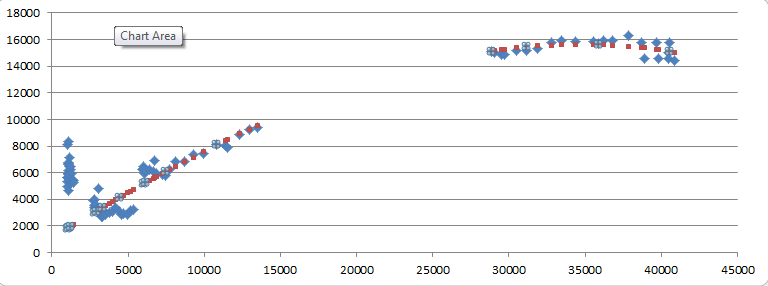
The graph below shows the scatterplot of actual values and the estimated line of the curve from the regression:

Using this model, we can estimate what the 5% reduction in GDP caused by a four month lockdown would mean in terms of life expectancy for the EU-28 countries. Here is what we get when we do that:
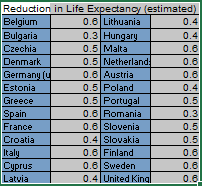
In summary, on average, a 5% reduction in GDP will result in a loss of an estimated 0.5 years, or 6 months, in the average life expectancy of people in Europe. This will happen because of many reasons, such as reduced spending on curative health, increased crime, more suicides, greater occupational risks and reduced spending in preventative health and safety.